Flight Route Optimizer

As part of the “Flight Operations Engineering” traject of my studies in Aviation, an assignment was given to implement optimization algorithms to optimize the lateral flight path of a route. The optimal route is dependant on the distance and the wind on a certain trajectory. Finding this optimal trajectory required the creation of a graph-like structure for a flight route between A and B and the implementation of an optimization algorithm that can find the optimal route in the graph.

To create a graph like structure, any route is split up into multiple waypoints divided by flight segments. At any waypoint, there are multiple paralel nodes, divided by a distance between 1 and 10 nautical miles. This forms a directed graph between the origin and the destination of the flight, as represented below. Any edge between two nodes has a weight appointed to it, based on the distance between the nodes, and the average wind. This corresponds to a flight time, and thus a fuel burn. A lower weight is better, as this equals less fuel used and less emissions.

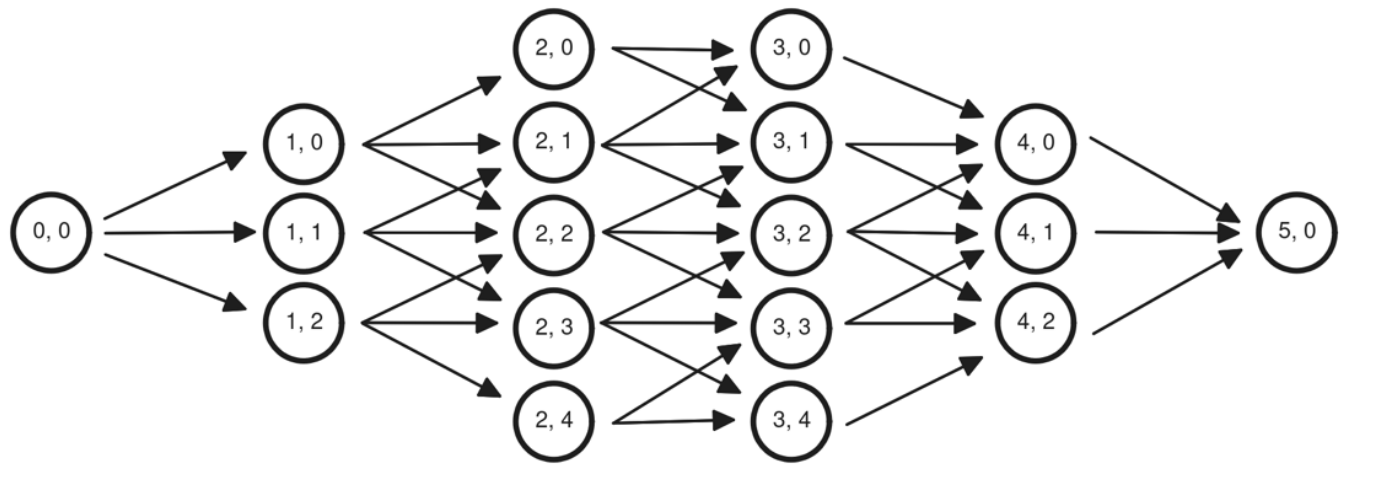
To find the shortest path in the graph, multiple algorithms were explored, with the limitation in mind that any implemented algorithms had to be coded from scratch, as imposed by the course guidelines. As an afterthought, this was a blessing in disguise, as experimenting with the prorgramming of these algorithms was enjoyable challenge. The expored algorithms are listed below:

• Breadth First Search (BFS)
• Dijkstra’s Algorithm
• A*
• Simulated Annealing

BFS, Dijkstra and A* are deterministic algorithms, meaning that it is guaranteed to always result in the same output: the optimal path. Simulated Annealing, however, is a meta-heuristic algorithm, which introduces randomness into the mix. This removes the guarantee of optimality, in turn bringing the benefit of a significantly shorter runtime. Because of this, Simulated Annealing was the overall winner, especially on larger routes where the deterministic algorithms started to struggle.